3968. Square root

Find such number x that x² + = C with no less than 6 digits after the decimal point.

Input. One real number C (1.0 ≤ C ≤ 10¹⁰).

Output. Print the root x with no less than 6 digits after the decimal point.

Sample input	Sample output
18.0	4.000000

SOLUTION

binary search

Algorithm analysis

Consider a function f(x) = x² + .

Its obvious that

· f(0) = 0;

· f(C) = C² + > C;

That is, the root of the equation

f(x) = С

lies on the interval [0; C]. Function f(x) is strictly increasing. Search for the root x with binary search.

Example

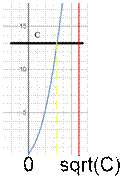
Consider the graph of the function f(x) = x² + . One can see that

· f(0) = 0 < C;

· f() = C+ > C;

Therefore, the root of equation f(x) = С lies on the interval [0; ] and can be found with binary search.

Algorithm realization

Declare a constant EPS and function f(x).

#define EPS 1e-10

double f(double x)

{

return x * x + sqrt(x);

}

The main part of the program. Read the value of С.

scanf("%lf",&c);

Set the boundaries of binary search [left; right] = [0; C].

left = 0; right = c;

Run the binary search.

while(right - left > EPS)

{

middle = (left + right)/ 2;

y = f(middle);

if (y > c) right = middle; else left = middle;

}

Print the answer.

printf("%lf\n",left);

Java realization

import java.util.*;

public class Main

{

static double f(double x)

{

return x * x + Math.sqrt(x);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

double c = con.nextDouble();

double left = 0, right = c;

while(right - left > 1e-10)

{

double middle = (left + right)/ 2;

double y = f(middle);

if (y > c) right = middle; else left = middle;

}

System.out.println(left);

con.close();

}

}